Numpy Dot Product: Calculate the Python Dot Product

In this tutorial, you’ll learn how to use Numpy to calculate the dot product in Python. Knowing how to understand and calculate the dot product between scalars and vectors is an important skill in machine learning. This post will go into detail as to what the dot product is and how to calculate it. You’ll learn how to calculate the dot product between two 1-dimensional arrays, a 1-dimension array and a scalar, and two 2-dimensional arrays.

The Quick Answer: Use numpy.dot()

What is the Dot Product?

The dot product, or the scalar product, takes two equal length vectors and returns a scalar. The dot product is shown, algebraically like this:

s = x ⋅ y

where:s is the dot product between two vectors, and x and y are two vectors.

This can be represented as:

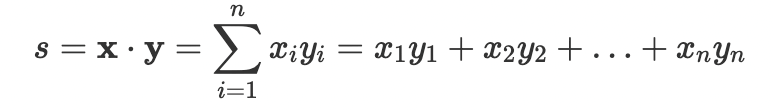
This tutorial will explore three different dot product scenarios:

1. Dot product between a 1D array and a scalar: which returns a 1D array
2. Dot product between two 1D arrays: which returns a scalar d
3. Dot product between two 2D arrays: which returns a 1D array

Let’s dive into learning how to use Python to calculate a dot product between a 1-dimensional array and a scalar.

Check out some other Python tutorials on datagy, including our complete guide to styling Pandas and our comprehensive overview of Pivot Tables in Pandas!

How to Use Numpy Dot to Calculate the Python Dot Product

numpy, the popular Python data science library comes with a number of helpful array functions. One of these functions, dot(), can be used to calculate the dot product across different scenarios, as you’ll learn in this tutorial.

The dot() product handles both dot product calculations and matrix multiplication, depending on the types of arrays and scalars that are passed into the function.

Let’s take a look at what the function looks like:

import numpy as np
dot = np.dot(x, y)

In the code above, we first imported numpy using the alias np. We can then access the dot() function, which accepts two required parameters, x and y in this case.

Depending on what data types are passed into the arguments, different calculations will happen – either dot products or matrix multiplication.

In the next section, you’ll learn how to use Python’s numpy to calculate the dot product between one 1-dimensional array and a scalar.

Want to learn how to calculate and use the natural logarithm in Python. Check out my tutorial here, which will teach you everything you need to know about how to calculate it in Python.

Calculate the Dot Product Between One 1-Dimensional Array and a Scalar

When you calculate the dot product between a 1-Dimensional array and a scalar unit, you essentially multiple each element in the array by the scalar.

Let’s take a look at an example. You’re given a 1-dimensional array [1, 2, 3] and a scalar 2. When you calculate the dot product between these two values, you multiply each value in the array by the scalar.

This then looks like this: [1x2, 2x2, 3x2].

Now that we understand what the dot product between a 1 dimensional vector an a scalar looks like, let’s see how we can use Python and numpy to calculate the dot product:

# Calculate the Dot Product in Python Between a 1D Vector and a Scalar
import numpy as np
x = 2
y = np.array([1, 2, 3])

dot = np.dot(x, y)
print(dot)

# Returns: [2 4 6]

We can see how easy numpy makes calculating the dot product between a scalar and a vector. Let’s break down what we’ve done here:

1. We instantiate two variables: x which represents a scalar, and y which represents a numpy array
2. We then calculate the dot product between the two by using the np.dot() function.
3. When we print the result, we can see that it returns a 1-dimensional array that contains the product of each value in the original array and the scalar.

In the next section, you’ll learn how to calculate the dot product between two 1-dimensional arrays using Python and numpy.

Want to learn more about calculating the square root in Python? Check out my tutorial here, which will teach you different ways of calculating the square root, both without Python functions and with the help of functions.

Calculate the Dot Product Between Two 1-Dimensional Arrays

When you calculate the dot product between two 1-dimensional arrays, a scalar value is returned. The way that this calculation is handled is to calculate the sum of the product of each value in the two arrays.

Because of this, the arrays must be the same size, otherwise the dot product cannot be calculated.

Let’s take a look at calculating the dot product between two arrays [2, 4, 6] and [3, 5, 7].

When we calculate the dot product of two 1-dimensional vectors, we calculate the vector multiplication of the fist vector and the transpose of the second.

For this, we calculate the following: [2 x 3 + 4 x 5 + 6 x 7], which reduces to [6 + 20 + 42] and returns the scalar 68.

Let’s see how we can calculate the dot product of two one-dimensional vectors using numpy in Python:

# Calculate the Dot Product in Python Between two 1-dimensional vectors
import numpy as np
x = np.array([2,4,6])
y = np.array([3,5,7])

dot = np.dot(x, y)
print(dot)

# Returns: 68

In the next section, you’ll learn how to calculate the dot product between two 2-dimensional arrays.

Want to learn more about Python for-loops? Check out my in-depth tutorial that takes your from beginner to advanced for-loops user! Want to watch a video instead? Check out my YouTube tutorial here.

Calculate the Dot Product Between Two 2-Dimensional Arrays

When you calculate a dot product between two 2-dimensional arrays, you return a 2-dimensional array. The way that this is calculated is using matrix multiplication between the two matrices.

Let’s take a look at an example where we have two arrays: [[1,2,3], [4,5,6]] and [[4,5,6], [7,8,9]]. This actually returns an array of size 2x2. This is because the dot product between two 2-dimensional arrays will always return a matrix the size of the number of rows of the first matrix and the number of columns of the second matrix.

Because of this, the size of the first matrix must be equal to the size of the transpose of the second matrix.

The way that this calculation will occur is shown below:

Now that we have an understanding of how the matrices will be multiplied, let’s take a look at how we can use Python and numpy to calculate the dot product.

# Calculate the Dot Product in Python Between two 2-dimensional matrices
import numpy as np
x = np.array([[1,2,3], [4,5,6]])
y = np.array([[4,5,6], [7,8,9]])

dot = np.dot(x, y.T)
print(dot)

# Returns: 
# [[ 32  50]
#  [ 77 122]]

Let’s explore what we’ve done here:

1. We loaded our two numpy arrays
2. We then applied the np.dot() function, passing in the first matrix and the transpose of the second.

If you want to learn more about calculating the transpose using numpy, check out my in-depth tutorial here.

In the next section, you’ll learn how to use the Python @ operator to calculate the dot product of numpy arrays.

Need to check if a key exists in a Python dictionary? Check out this tutorial, which teaches you five different ways of seeing if a key exists in a Python dictionary, including how to return a default value.

Use @ To Calculate the Python Dot Product

Beginning in Python 3.5+, there is an operator that allows you to calculate the dot product between two arrays, the @ operator. The operator leverages different libraries, such as numpy, to support the calculation of a dot product.

While this approach still uses numpy, it can help simplify the process of calculating a dot product. By using an operator, we’re simplifying the approach and making it more syntactic.

Rather than using the np.dot() function, then, we can use the @ operator as we did with the above example.

Want to learn how to get a file’s extension in Python? This tutorial will teach you how to use the os and pathlib libraries to do just that!

Calculate the Dot Product Between Two 1-Dimensional Arrays Using @

Let’s see how we can replicate our example of calculating the dot product between a scalar and a 1-dimensional array using the @ operator:

# Calculate the Dot Product in Python Between two 1-dimensional vectors
import numpy as np
x = np.array([2,4,6])
y = np.array([3,5,7])

dot = x @ y
print(dot)

# Returns: 68

In the next section, you’ll learn how to use the @ operator to calculate the dot product of two 2-Dimensional arrays in Python.

Want to learn how to use the Python zip() function to iterate over two lists? This tutorial teaches you exactly what the zip() function does and shows you some creative ways to use the function.

Calculate the Dot Product Between Two 2-Dimensional Arrays Using @

Now let’s take a look at how we can use the @ operator to calculate the dot product between two 2-dimenionsla arrays.

# Calculate the Dot Product in Python Between two 2-dimensional vectors using @
import numpy as np
x = np.array([[1,2,3], [4,5,6]])
y = np.array([[4,5,6], [7,8,9]])

dot = x @ y.T
print(dot)

# Returns: 
# [[ 32  50]
#  [ 77 122]]

We can see here that this returns the same result.

Need to automate renaming files? Check out this in-depth guide on using pathlib to rename files. More of a visual learner, the entire tutorial is also available as a video in the post!

Conclusion

In this tutorial, you’ll learned how to calculate the dot product in Python. You learned what the dot product represents and three different cases in which the dot product can be calculated: between a scalar and an array, between two 1-dimensional arrays, and between two 2-dimensional arrays.

You learned how to use the numpy dot() function as well as the @ operator available in Python 3.5.

To learn more about the numpy dot() function, check out the official documentation here.