In this tutorial, you’ll learn how calculate the Python e, or the Euler’s Number in Python. The number is equal to approximately 2.71828, and represents the base of the natural logarithm. The number is also often used in calculating compound interest and other natural phenomena.
You’ll learn how to use the Python math library to calculate the Euler number, e. This can be done use the built-in constant math.e as well as the function math.exp().
The Quick Answer: Use math.e
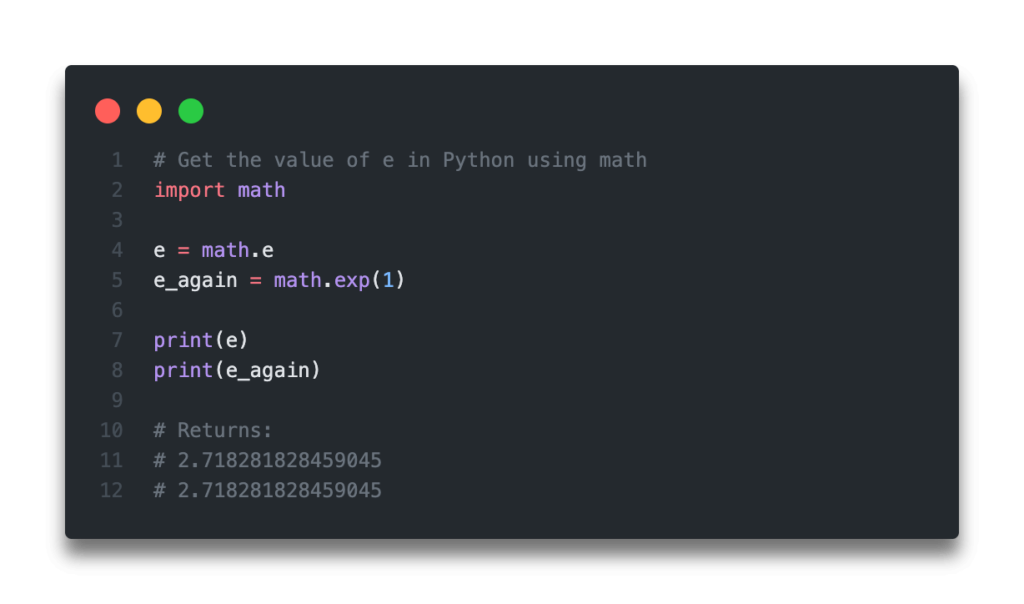
Table of Contents
What is Euler’s Number?
Euler’s number, often referred to simply as e, is a mathematical constant that serves many purposes, including in calculating compound interest. The number is found in many natural phenomena and, because of this is found in many different mathematical calculations.
For example, the value e is used so often in calculating logarithms that the natural logarithm, which uses e as its base, is simply referred to as ln(). The constant is used frequently in compound interest, standard normal distributions, and in calculus.
The value of e is roughly 2.71828, but the more precise the value is, the more accurate your calculations will be. Because of this, it’s helpful to use the constant value or calculate it from scratch.
In the next section, you’ll learn how to use the Python math library to use the constant for the value of e.
Check out some other Python tutorials on datagy, including our complete guide to styling Pandas and our comprehensive overview of Pivot Tables in Pandas!
How to Use Python Math to Find the e Constant
The Python math library comes packaged with a number of important constants, among them pi and e.
Because we need to reference these values often, it can be important to know how to access them.
Let’s see how we can access the value for e using the math library:
# Print the value of e with math.e
import math
e = math.e
print(e)
# Returns: 2.718281828459045Let’s see what we’ve done here:
- We imported the
mathlibrary - We access the constant by using the
.esuffix
In the next section, you’ll learn how to use math.exp() function to calculate Euler’s number.
Want to learn more about calculating the square root in Python? Check out my tutorial here, which will teach you different ways of calculating the square root, both without Python functions and with the help of functions.
How to Use the Python Math Exp Function to Calculate Euler’s Number
The math library comes with a function, exp(), that can be used to raise the number e to a given power.
Say we write exp(2), this would be the same as writing e2.
Let’s take a look at how we can use Python to do this:
# Print the value of e with math.exp()
import math
print(math.exp(2))
# Returns: 7.38905609893065The Python documentation actually notes that using the math.exp() function may be a more accurate way of getting the value of e.
Since the we can use the math.exp() function to raise e to a provided power, we can actually just pass the value of 1 into the function to return the value of e.
Let’s see how we can do this using Python and the math library:
# Print the value of e with math.exp()
import math
print(math.exp(1))
# Returns: 2.718281828459045In the next section, you’ll learn how to use Python and the math library to use the value of e to calculate a natural logarithm.
Want to learn how to use the Python zip() function to iterate over two lists? This tutorial teaches you exactly what the zip() function does and shows you some creative ways to use the function.
How to Use e to Calculate the Natural Logarithm in Python
One special logarithm often used in many practical real-world problems is to use what is known as the natural logarithm. Because the use of the natural logarithm is so common, it’s given a special way of being written ln(), which is the same as writing loge().
Now that we know how to get the value of e, we can now calculate a natural logarithm in Python:
# Calculate the natural logarithm with math
import math
value1 = math.log(1, math.e)
value2 = math.log(2, math.e)
value3 = math.log(3, math.e)
print(value1)
print(value2)
print(value3)
# Returns
# 0.0
# 0.6931471805599453
# 1.0986122886681098Now, one interesting thing to note is that when no base is passed into the math.log() function, it defaults to the value of e. Because of this, we don’t actually need to pass it into the function.
Let’s verify this by passing in a few test items to see if we get the same values as indicated above:
# Calculate the natural logarithm with math
import math
value1 = math.log(1)
value2 = math.log(2)
value3 = math.log(3)
print(value1)
print(value2)
print(value3)
# Returns
# 0.0
# 0.6931471805599453
# 1.0986122886681098We can see that this returns the same values!
Want to learn how to calculate and use the natural logarithm in Python. Check out my tutorial here, which will teach you everything you need to know about how to calculate it in Python.
Conclusion
In this tutorial, you learned how to use Python to calculate and use the value of e, Euler’s number. You learned how to use the Python math library which comes with a constant value as well as a function to calculate the value from scratch. You also learned how to use the Python e constant to calculate the natural logarithm.
To learn more about the Python math library, check out the official documentation here.

