Tanh Activation Function for Deep Learning: A Complete Guide

In this comprehensive guide, you’ll explore the Tanh activation function in the realm of deep learning. Activation functions are one of the essential building blocks in deep learning that breathe life into artificial neural networks. The Tanh activation function is particularly useful for recurrent neural networks or multi-class classification tasks, such as those in computer vision problems.

By the end of this tutorial, you’ll have learned the following:

• What the Tanh activation function is
• How to implement the Tanh activation function in PyTorch, the essential deep learning framework in Python
• What the pros and cons of the Tanh activation function are
• How the Tanh function relates to other deep learning activation functions

Understanding the Tanh Activation Function

The Tanh (Hyperbolic Tangent) activation function is one of the fundamental activation functions for deep learning. In this section, we’ll explore the inner workings of the function. Let’s take a look, first, at the mathematical representation of the Tanh activation function:

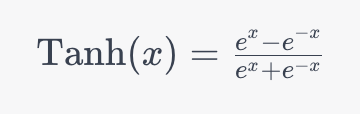
In the function above, e represents the mathematical constant Euler’s number and x is the input to the function. The function allows you to map any value from positive infinity to negative infinity to an output in the range of -1 to +1.

Now that you know how to define the function, let’s take a look at some of the important characteristics of the Tanh activation function:

1. Symmetry: the Tanh activation function is symmetrical around the origin (0, 0), meaning that Tanh(-x) = -Tanh(x). This can be particularly helpful when dealing with data that is naturally centered around zero.
2. Zero-centered: the Tanh activation function is centered around zero, meaning that it has an output mean of zero. This allows it to help address the vanishing gradient problem. It helps prevent the problem because gradients are not consistently positive or negative, allowing for more stable weight updates.
3. Range: Because the function outputs values between -1 to 1, it can be helpful when working with data that has both positive and negative aspects to the outputs.

Now that you know how to define the Tanh function and have an understanding of some of its main characteristics, let’s dive into the use cases and applications of the function.

Use Cases and Applications of the Tanh Activation Function

The Hyperbolic tangent function has many unique characteristics, which lends itself to many practical applications in different domains. In this section, you’ll explore some of the use cases and applications of the Tanh activation function:

1. Hidden layers of feedforward neural networks: Tanh is a frequently used function in hidden layers of feedforward neural networks. Because it’s zero-centered, it allows networks to handle both positive and negative input values, which can lead to more stable weight updates and improved convergence.
2. Recurrent Neural Networks (RNNs): The zero-centered property helps in capturing and propagating long-term dependencies in sequential data, such as natural language processing and time series analysis.
3. Long Short-Term Memory (LSTM) Networks: LSTM networks were developed to address the vanishing gradient problems in RNNs. Tanh activation functions play a significant role in LSTM units, which enable the network to regulate information flow and memory storage.
4. Convolutional Neural Networks (CNNs): The Rectified Linear Unit (ReLU) Function is a popular choice for CNNs, but Tanh can be a helpful function when input data has been normalized. This allows the neural network to capture both positive and negative features, which can be beneficial for image recognition and analysis.

Now that you have a solid understanding of the uses of the Tanh function, let’s take a look at how you can implement the function in PyTorch.

Implementing the Tanh Activation Function in PyTorch

PyTorch is a popular deep-learning framework for building neural networks in Python. The framework makes it easy to implement the Tanh function using the nn module. In this section, we’ll explore how to implement the function. Let’s begin by importing the library and the nn module.

# Importing Our Libraries
import torch
import torch.nn as nn

Now that we have the libraries imported, we can instantiate the function by calling the nn.Tanh class. Let’s see what this looks like:

# Instantiating the Tanh Function
tanh = nn.Tanh()

We can now call the function using the new tanh function object we created. Let’s now create a new sample tensor, which we can transform using the tanh function.

# Transforming a Tensor Using tanh
data = torch.tensor([-3.0, -2.0, -1.0, 0.0, 1.0, 2.0, 3.0])
transformed = tanh(data)
print(transformed)

# Returns:
# tensor([-0.9951, -0.9640, -0.7616,  0.0000,  0.7616,  0.9640,  0.9951])

In the code block above, we created a tensor containing values from -3 to +3. We then passed this tensor into our new function object and printed the results.

We can see from the resulting tensor that our results are symmetrical, meaning that the transformed value of 3, is the same negative value.

Advantages of the Tanh Activation Function Function for Deep Learning

In this section, we’ll explore the key benefits and advantages of the Tanh activation function for deep learning. This will give you a solid understanding of why the function remains a popular method of activating your neural networks.

1. Zero-centered output: Unlike the ReLU function and its variants, which are primarily positive and lack negative values, Tanh produces outputs that are centered around zero. This simplifies the optimization process by mitigating the vanishing gradient problem, by stabilizing weight updates.
2. Symmetry: The function is symmetrical with respect to the origin, which simplifies the network’s learning process by capturing negative and positive values equally. In scenarios where data has both positive and negative patterns (such as image recognition or speech recognition), the Tanh activation function helps a network learn these aspects more effectively.
3. Bounded output range: because the Tanh function squashes an input value to a range of -1 to +1, the function can be beneficial when dealing with data that has well-defined limits. This can be useful when the output must be constrained.
4. Capturing negative and positive patterns: because Tanh can capture both positive and negative patterns in data, the function can be useful for capturing relationships that carry both negative and positive values.
5. Smoothness: The Tanh function is smooth and continuously differentiable. This smoothness can aid gradient-based optimization algorithms like stochastic gradient descent (SGD) in converging to a good solution, as gradients are well-behaved and changes in the output are gradual.

In this section, you learned five of the main advantages of the Tanh activation function. In the following section, we’ll explore some of the limitations of the function.

Limitations of the Tanh Activation Function Function for Deep Learning

In the previous section, we made a compelling case of the Tanh activation function. However, it’s not all sunshine and roses. In this section, we’ll take a look at the main limitations or disadvantages of the Tanh activation function:

1. Vanishing Gradient Problem: The Tanh activation function mitigates the vanishing gradient problem better than the sigmoid function but not as effectively as the Rectified Linear Unit (ReLU). The gradients tend to be smaller in the outer regions of the Tanh curve, which can slow down training, particularly in deep networks.
2. Computational Cost: Calculating the Tanh function involves computing exponentials and divisions, which are relatively more computationally expensive compared to the simpler ReLU activation or its variants. In large-scale deep learning applications, this added computational cost can be a limiting factor.
3. Output Range Constraints: While the bounded output range of Tanh can be an advantage in some cases, it can also be a limitation in situations where the data does not naturally lie in the -1 to 1 range.

By balancing the advantages and limitations of the Tanh activation function, you can evaluate whether or not it’s the most appropriate function for the problem you are trying to solve!

Comparing Tanh and Other Activation Functions

In this section, we’ll compare the Tanh activation function to other functions, such as the ReLU or the Sigmoid activation function.

Functions	Similarities	Differences
Tanh vs. Sigmoid	Tanh and the Sigmoid function share some characteristics, including being bounded within a range, zero-centered at their origin, and smooth.	Tanh ranges from -1 to 1, while the Sigmoid ranges from 0 to 1. Tanh generally produces larger gradients, which can help with mitigating the vanishing gradient problem more effectively.
Tanh vs. ReLU	Both Tanh and ReLU are zero-centered, which helps with vanishing gradient issues. However, ReLU is unbounded from above, while Tanh is bounded within the -1 to 1 range.	ReLU is known for being computationally efficient and, in practice, often leads to faster convergence. However, it can suffer from the “dying ReLU” problem, where neurons become inactive during training.
Tanh vs. Leaky ReLU	Like ReLU, Leaky ReLU addresses the vanishing gradient problem and allows gradients to flow during training. Both are computationally efficient.	Tanh is zero-centered, while Leaky ReLU introduces a small non-zero gradient for negative inputs. Leaky ReLU is often favored in scenarios where you want to maintain some level of gradient flow for all inputs, especially if negative values are important for the task.
Tanh vs. Softmax	Tanh and the Softmax activation function are both smooth, continuous functions that map inputs to specific output ranges. Softmax is typically used for multi-class classification tasks.	Tanh produces output values in the range of -1 to 1, making it suitable for tasks that require handling both positive and negative values. In contrast, Softmax is specifically designed for multi-class classification problems and converts a vector of real numbers to a probability distribution over multiple classes.

Now that you have a solid understanding of how the Tanh function compares to other activation functions, you can more confidently decide when to use which function.

The Tanh activation function is most commonly used in recurrent neural networks (RNNs) and long short-term memory (LSTM) networks due to its zero-centered nature. This is because it helps capture long-term dependencies. Similarly, it’s also important in specific applications where negative and positive patterns exist, such as speech recognition or natural language processing.

Conclusion

In this comprehensive guide, we delved into the world of the Tanh activation function and its relevance in the realm of deep learning. Activation functions are the core components that bring neural networks to life, and the Tanh activation function, with its unique characteristics, serves a significant role in specific applications, such as recurrent neural networks (RNNs) and multi-class classification tasks, particularly in computer vision problems.

The Tanh activation function’s zero-centered property, versatility, and unique advantages make it a valuable tool in deep learning. By carefully considering the characteristics and requirements of your data and neural network architecture, you can harness the potential of the Tanh activation function for a wide range of applications.

In conclusion, the Tanh activation function’s ability to handle both positive and negative values, coupled with its symmetric nature, positions it as a key player in the realm of deep learning, contributing to the development of sophisticated neural network models that excel in capturing intricate patterns and dependencies in data.

To learn more about the Tanh activation function in PyTorch, check out the official documentation.