Softmax Activation Function for Deep Learning: A Complete Guide

In this comprehensive guide, you’ll explore the softmax activation function in the realm of deep learning. Activation functions are one of the essential building blocks in deep learning that breathe life into artificial neural networks. The softmax activation function is particularly useful for multi-class classification tasks, such as those in computer vision problems.

By the end of this tutorial, you’ll have learned the following:

• What the softmax activation function is and how it produces probabilities for multi-class classification tasks
• How to implement the softmax activation function in PyTorch, the essential deep learning framework in Python
• What the pros and cons of the softmax activation function are
• How the function relates to other deep learning activation functions

Understanding the Softmax Activation Function

The softmax activation function is designed to work with multi-class classification tasks, where an input needs to be assigned to one of several classes. The function is used to transform raw, unbounded scores (which are often referred to as logits) into a probability distribution over multiple classes. This means that it assigns probabilities to each class, indicating how likely it is that an input belongs to that class.

The softmax function uses a vector of real numbers as input and returns another vector of the same dimension, with values ranging between 0 and 1. Because these values add up to 1, they represent valid probabilities.

Let’s take a look at the mathematical formula for the softmax activation function:

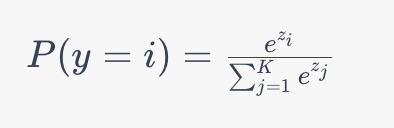
In the formula above:

• P(y=i) is the probability that the input belongs to the class
• z_i, is the raw score or logit for class
• The denominator is the sum of exponentiated logits for all classes, ensuring the output is a valid probability distribution.

The function is used to make predictions in multiclass classification problems. The function assigns higher probabilities to classes with higher logits, which allows you to select the most likely class.

Now that you have a good sense of how the function works, let’s dive into the use cases and applications of the softmax activation function.

Use Cases and Applications of the Softmax Activation Function

The strength of the softmax activation function is the ability to transform raw scores into meaningful probability distributions. This means it’s incredibly valuable to use for multi-class classification problems. In this section, we’ll explore some of the main use cases for the powerful softmax activation function:

1. Image classification: the softmax activation function plays a pivotal role in image classification tasks. It’s usually used in the final layer of a convolutional neural network (CNN), which can help you discern images between dogs, cats, and airplanes.
2. Natural language processing: when working on natural language processing (NLP) tasks, the softmax activation function can be very helpful for text classification problems or sentiment analysis. This works by assigning a score to different categories based on the text’s input features.
3. Speech recognition: the tools that power voice assistants such as Siri and Google Assistance often rely on deep learning techniques that incorporate softmax. By using an acoustic feature map, deep learning models turn features of spoken words into linguistic representations using classifications created from predefined vocabularies.

These applications of the softmax activation function represent just a small sampling of everything that is possible with the function. Let’s now turn our attention to how we can implement the powerful function in the popular deep learning framework, PyTorch.

Implementing the Softmax Activation Function in PyTorch

In this section, we’ll explore how to implement the softmax activation function in PyTorch. PyTorch is one of the most popular and versatile deep-learning frameworks available. The framework easily allows you to incorporate the softmax activation function into your neural network architectures.

The softmax activation function is implemented in PyTorch using the nn.Softmax() class. Let’s take a look at how we can implement the function:

# Implementing the Softmax Activation Function in PyTorch
import torch
import torch.nn as nn

softmax = nn.Softmax(dim=1)

In the code block above, we imported both the torch library and its nn module. We then created a new function object, softmax, by instantiating the nn.Softmax() class.

The class also allows you to customize the dimension along which Softmax should be computed by modifying the dim= parameter. This means that every slice along the dimension will sum to 1. Previously, PyTorch was able to handle this implicitly but now encourages explicit dimension declaration.

Let’s now see how we can use the function. Normally, you’d apply this function to the output of the last layer of your network, where you receive raw logits. Logits are the unnormalized predictions of a model, which in this case are simply the output of your last layer.

Let’s create a sample tensor containing our raw logits and convert it into predictions:

# Using the SoftMax Activation Function
# Sample logits
logits = torch.tensor([[2.0, 1.0, 0.1],
                       [0.2, 1.9, 3.0]])

# Apply softmax
softmax_probs = softmax(logits)
print(softmax_probs)

# Returns:
# tensor([[0.6590, 0.2424, 0.0986],
#         [0.0436, 0.2388, 0.7175]])

In the example above, we created a sample tensor using the torch.tensor() function. We then passed out logits into the our softmax function, returning a tensor of the same shape with predicted probabilities for each class. Because we used dim=1, the values along the first dimension add up to 1.

We can now use the PyTorch’s argmax function to get the predicted class of each record. Let’s see how we can accomplish this:

# Get predicted classes
predicted_classes = torch.argmax(softmax_probs, dim=1)

print("Softmax Probabilities:")
print(softmax_probs)
print("Predicted Classes:")
print(predicted_classes)

# Returns:
# Softmax Probabilities:
# tensor([[0.6590, 0.2424, 0.0986],
#         [0.0436, 0.2388, 0.7175]])
# Predicted Classes:
# tensor([0, 2])

In the code block above, we passed our probabilities into the argmax function. This returns the index of the maximum value along each dimension (which, in this case is 1). We can see from our sample data that the first record belongs to class 0, while the second belongs to class 2.

Advantages of the Softmax Activation Function Function for Deep Learning

In this section, we’ll take a look at some of the most important advantages of the softmax activation function for deep learning. Let’s dive right into these advantages:

1. Probabilities interpretation: the softmax activation function is able to convert raw logits into a probabilistic interpretation of model predictions. This allows you to more easily understand the confidence in a model’s predictions, which can be particularly useful when you want to not only know a class but also the level of certainty associated with it.
2. Multiclass Classification: the softmax activation function is specifically made for multiclass classification tasks and handles each of these with ease. It does this by assigning probabilities to each class.
3. Gradient-based Optimization: the function plays well with gradient-based optimization techniques, such as stochastic gradient descent. Because it is smooth and has a differentiable output, the gradients can be calculated efficiently during backpropagation.
4. Regularization Effect: the function has an inherent regularization effect. This is because the sum of probabilities must equal 1, which encourages the model to distribute probabilities more evenly. This can help prevent overfitting.

Now, let’s dive into some of the limitations of the function.

Limitations of the Softmax Activation Function Function for Deep Learning

While the softmax activation function has many advantages, it also has its own limitations. Let’s explore the limitations of the softmax activation function below:

1. Sensitivity to Scale: the function is sensitive to the scale of the inputs. If the magnitudes of the raw scores (or logits) are significantly different, then the resulting probabilities can be dominated by the largest scores. This can lead to vanishing gradients which can slow down or impede training.
2. Lack of margin information: because the function assigns probabilities based solely on relative magnitudes, it doesn’t consider the margin or gap between logits.
3. Risk of overfitting: when working with small datasets, the function can lead to overfitting. This happens because the function tends to produce confident predictions, which may fit to the noise of the training data, rather than the signal.
4. Computationally Expensive: when working with a large number of classes, the function can be computationally expensive due to the exponentiation of logits.
5. Not Well-Suited for Imbalanced Data: in situations where there are classes are highly imbalanced, softmax can bias a model towards the majority class. This occurs because the function attempts to normalize the class probabilities based on the training data distribution.

In the following section, we’ll explore how the function compares to other activation functions.

Comparing Softmax and Other Activation Functions

Because there are so many different activation functions available, it’s important to consider when to use which function. In this section, we’ll explore how the softmax activation function compares to other activation functions and when it’s best to use one function over another.

Softmax Activation Function vs. ReLU Activation Function

The softmax activation function is best used for multi-class classification problems applied to the final layer of the network. On the other hand, the ReLU activation function is best suited for hidden layers in deep neural networks. It’s also computationally lightweight, especially when compared to the softmax activation function. However, the ReLU function does not produce probabilities, making it more difficult to use for a final prediction layer.

Softmax Activation Function vs. Sigmoid Activation Function

When comparing the softmax and sigmoid activation functions, it’s important to note that both can be used for multi-class classification tasks. The key difference is that while the softmax activation function generates probabilities for multiple, mutually exclusive classes, it is commonly used in tasks where each input belongs to only a single class.

On the other hand, the sigmoid activation function can be used for either binary classification tasks or multi-label classification. Because the function maps logits to the [0,1] range, it can provide class probabilities independently of one another. This allows it to be more suitable for problems when inputs can belong to multiple classes.

Softmax Activation Function vs. Tanh Activation Function

The softmax activation function will always produce probabilities for multiple classes that add up to 1, making it most suitable for multi-class classification tasks. The Tanh function, on the other hand, maps inputs to the [-1, 1] range, which can be particularly helpful for recurrent neural networks and some feed-forward networks.

Because of this, the difference is a bit more straightforward: use the softmax activation function for multi-class classification tasks and the Tanh function for recurrent neural networks, or when you need the outputs to be between -1 and 1.

Conclusion

The softmax activation function is a fundamental component of the deep learning paradigm, especially in multi-class classification tasks. Because the function can convert raw scores into meaningful probabilities, it has become an indispensable tool in various domains, including computer vision and natural language processing.

In this guide, we first explored the fundamental principles of the softmax activation function by exploring its mathematical formulation. We then dove into how to implement the function using the popular deep learning framework, PyTorch. From there, we explored the benefits and drawbacks of the function. We closed off the tutorial by exploring how the function compares to alternative activation functions, including the ReLU and sigmoid.

To learn more about the PyTorch implementation, check out the official documentation.